Detonation wave at elevated pressure
Focus on the initiation, structure and stability of gaseous detonation at high preassure where real gas effects are non-negligible.
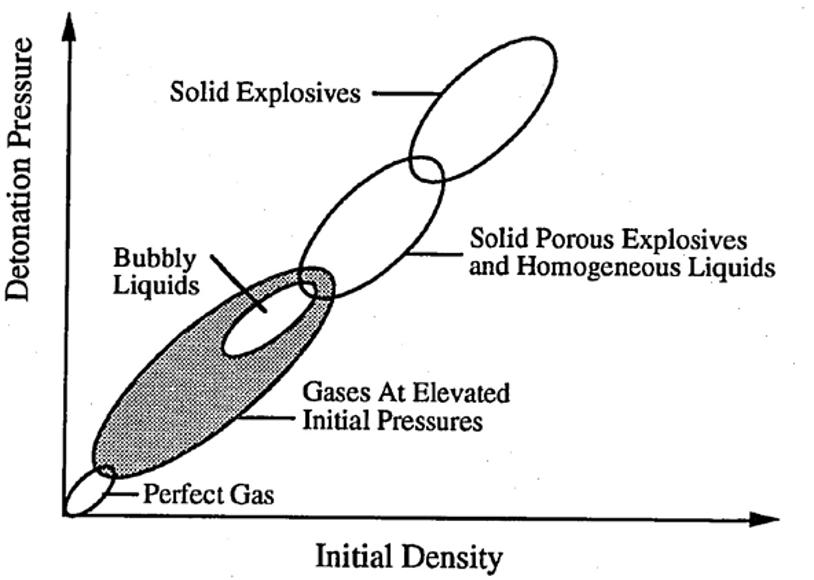
The research on detonation can be seperated into several regimes using the pressure and density diagram of Schmitt and Bulter [1]. Gas phase detonation focus mainly on low pressure regime with perfect gas assumption while solid explosive or energetic materials lie on high pressure regime. Recently, the research on two-phase RDE partly falls in the regime of liquid phase detonation. However, the regime of gas with elevated pressure seems rarely explored in detonation research, which is relevant to the safety of high pressure energy or combustion devices. It has been proved that the perfect gas based model fails to capture the detonation speed and cellular structure regularity at elevated pressure [1-2].
1. Detonation initiation
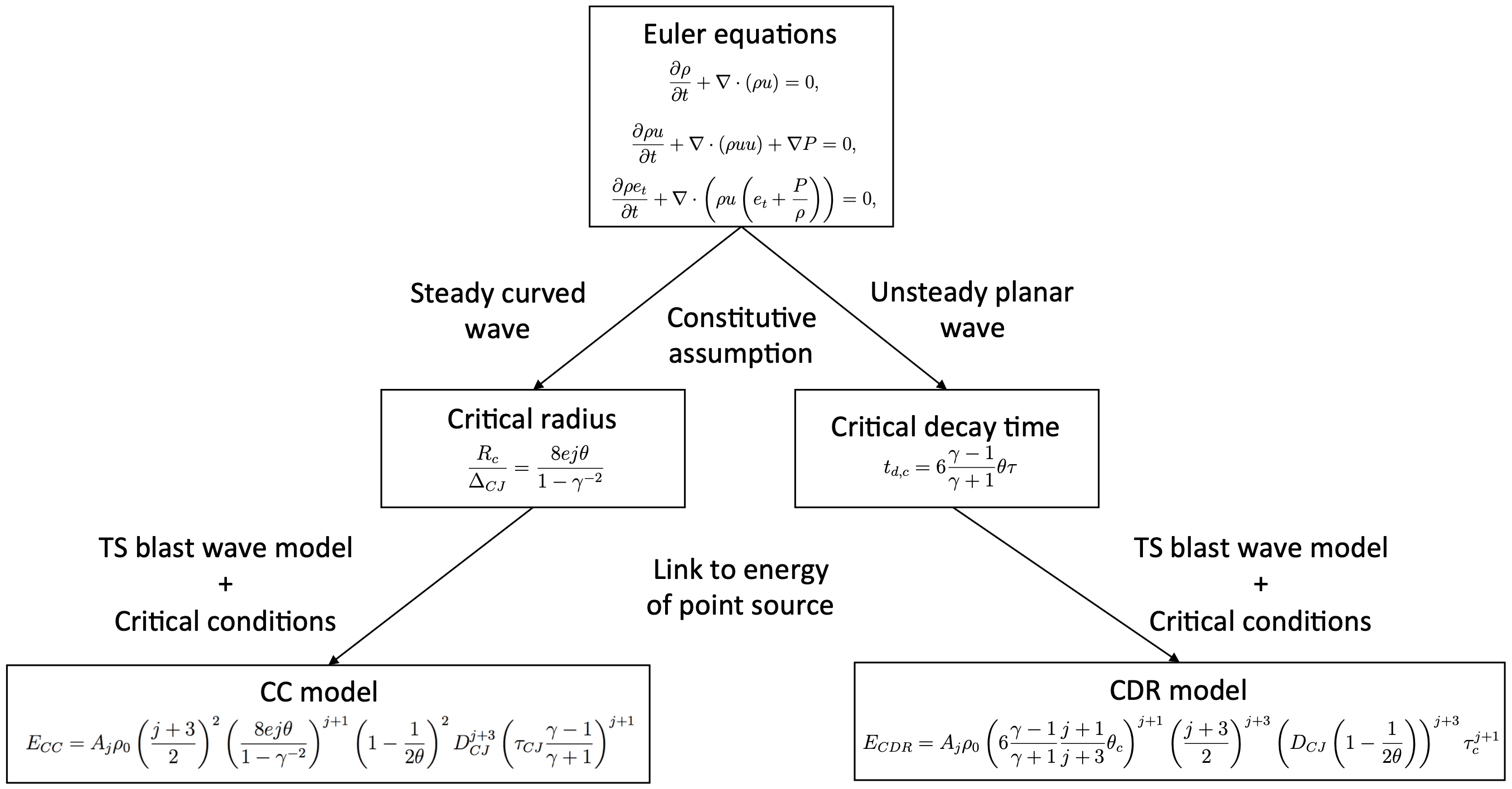
Detonation can be initiated by the rapid release of energy from a point energy source, which is referred to as direct detonation initiation (DDI). Prediction on the critical state of direct detonation initiation is a fundamental problem. The critical curvature (CC) theory [3] assumes curvature is the quenching mechanism and unsteadiness is negligible for DDI. In contrast, the critical decay rate (CDR) theory [4] assumes the unsteadiness to be the dominant quenching effects.
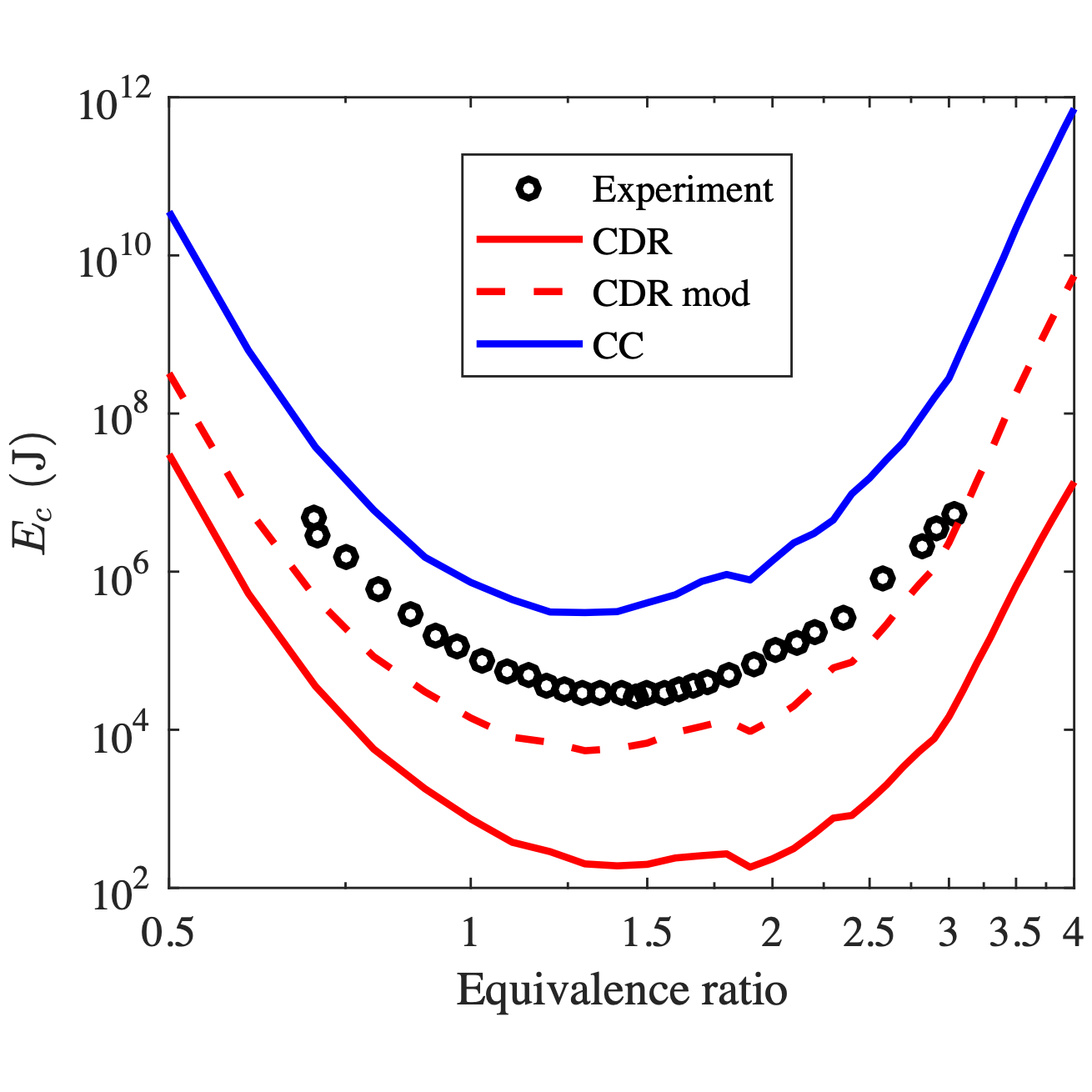
We proposed a fair comparison of the two models. We demonstrated that the critical conditions of the CDR model can be fulfilled more easily than those of the CC model. The critical initiation energy calculated with the CC and CDR models was found to be one to two orders of magnitud, with the CDR model more consistent with experimental data.
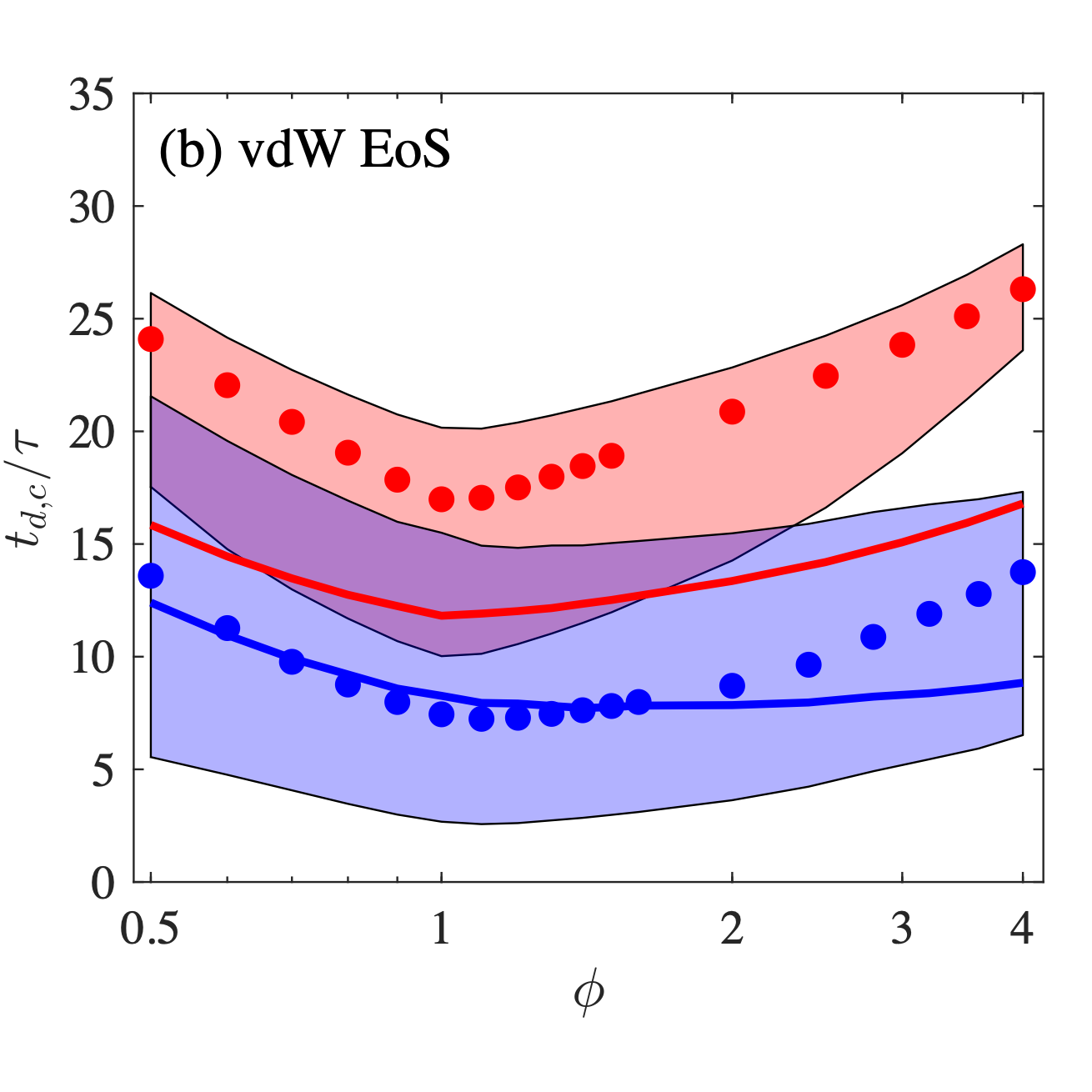
To study the critical state of DDI at elevated initial pressure, the critical decay rate model was extended from perfect gas to real gas to evaluate the real gas effects. Real gas models based on Noble-Abel and van der Waals equation of state were considered and approximated analytical solutions were obtained. Compared to the perfect gas based results, the finite molecular volume results in easier initiation while the inter-molecular interaction results in more difficult initiation.
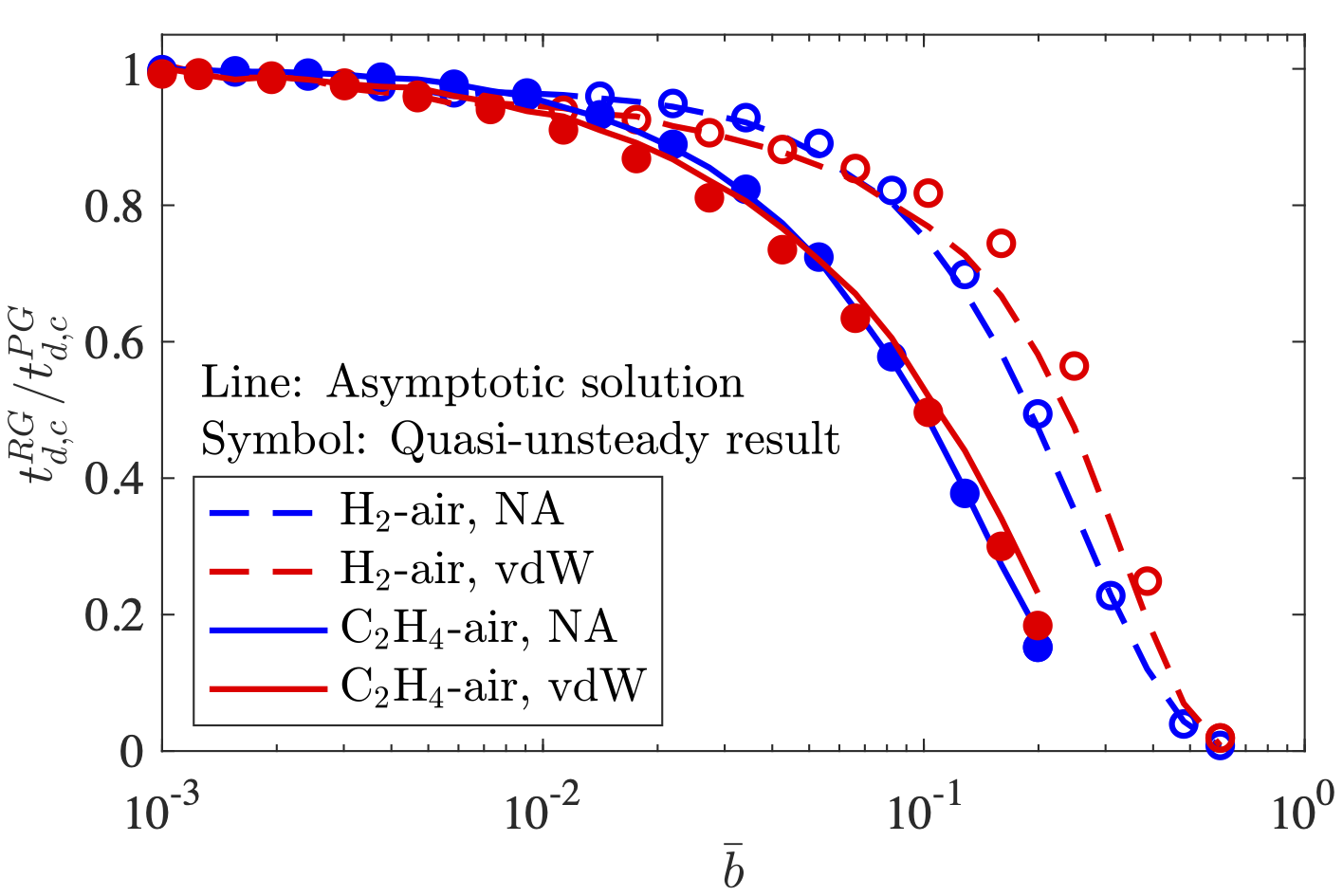
2. Detonation structure
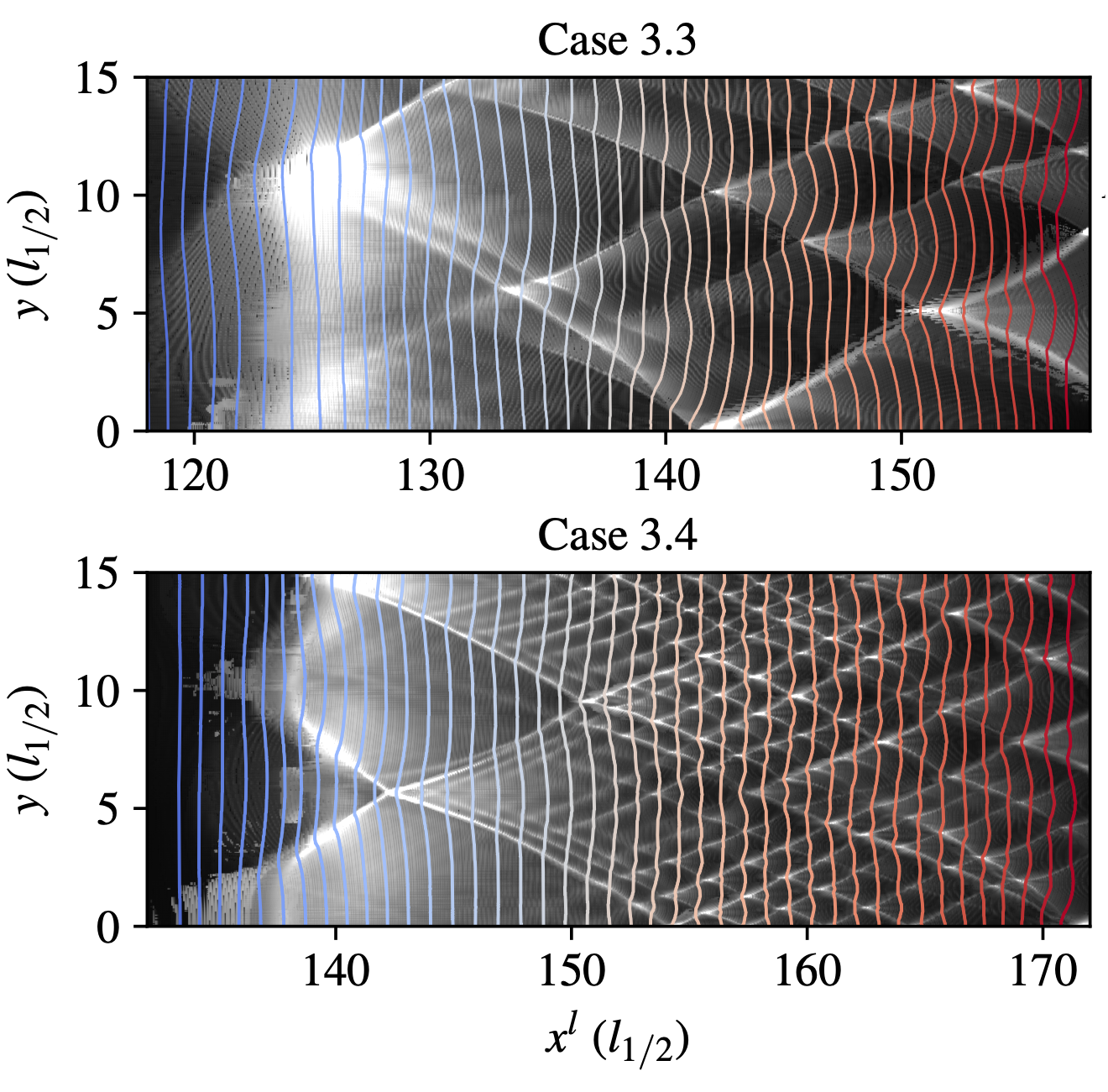
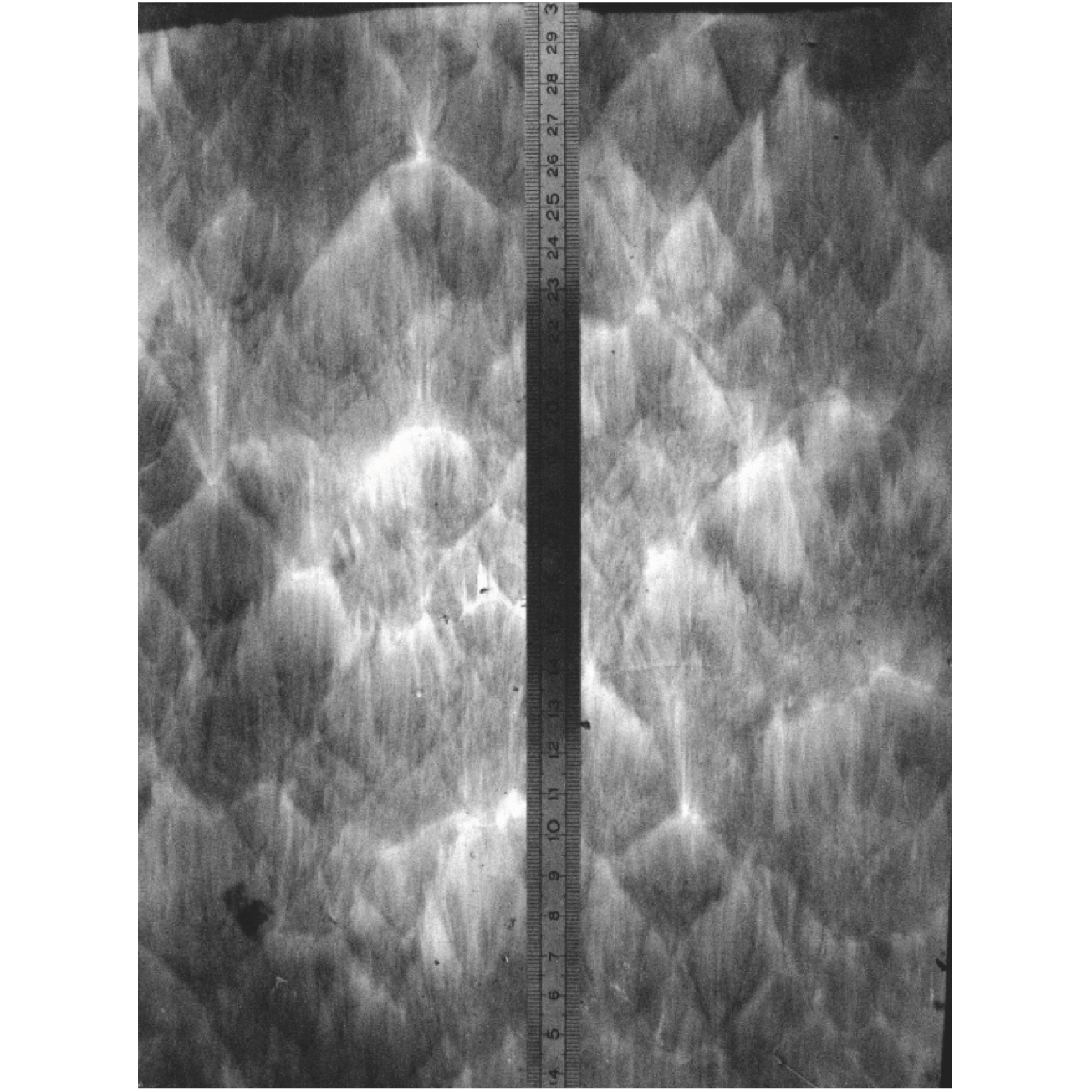
Detonation wave is characterized by multi-scale structures. The reaction zone structure governs the heat release which coupled with the shock dynamics. The detonation front constitutes of many groups of triple-shock wave, i.e. Mach stem, incident shock and transvere shock connecting via a triple point. The trajectory of triple point forms the cellular structure that could be measured with sootfoil technique in experiments.
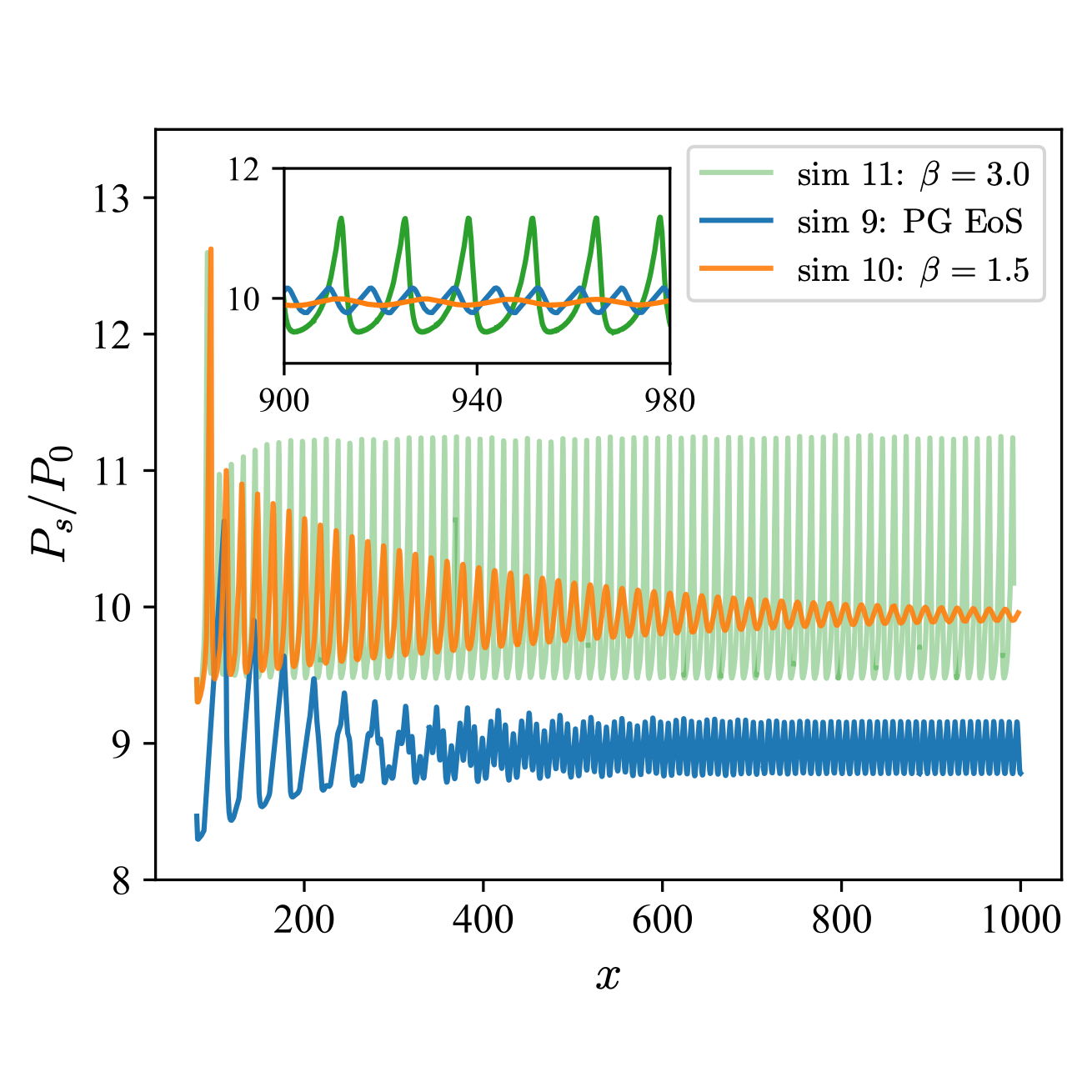
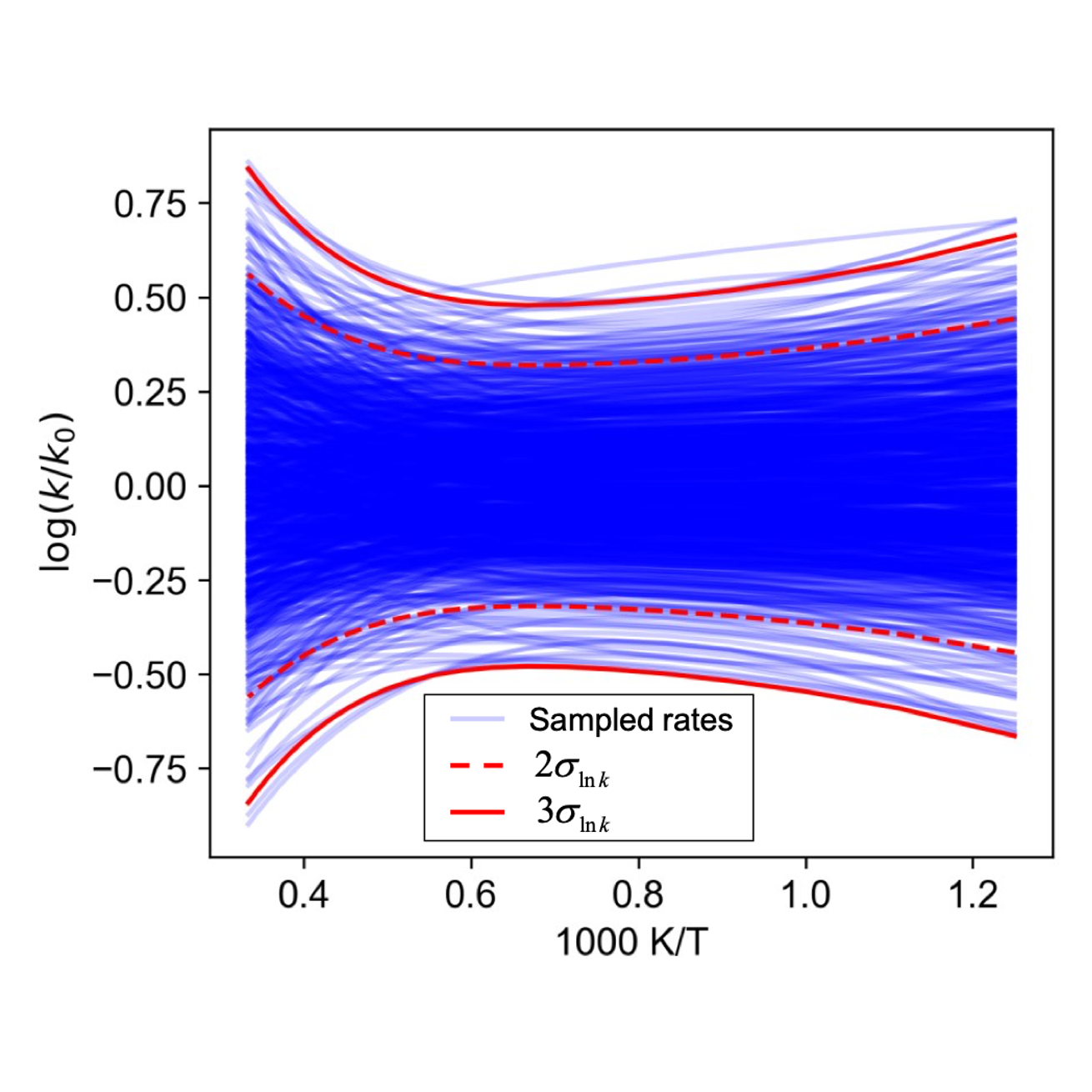
The detonation speed, reaction zone structure of steady detonation wave were studied for both perfect gas and real gas models. Larger detonation speed was obtained for real gas model which agrees better with experimental data. The reaction zone structure depends on various aspects in the real gas model. In addition, uncertainty quantification was performed for parameters in real gas model.
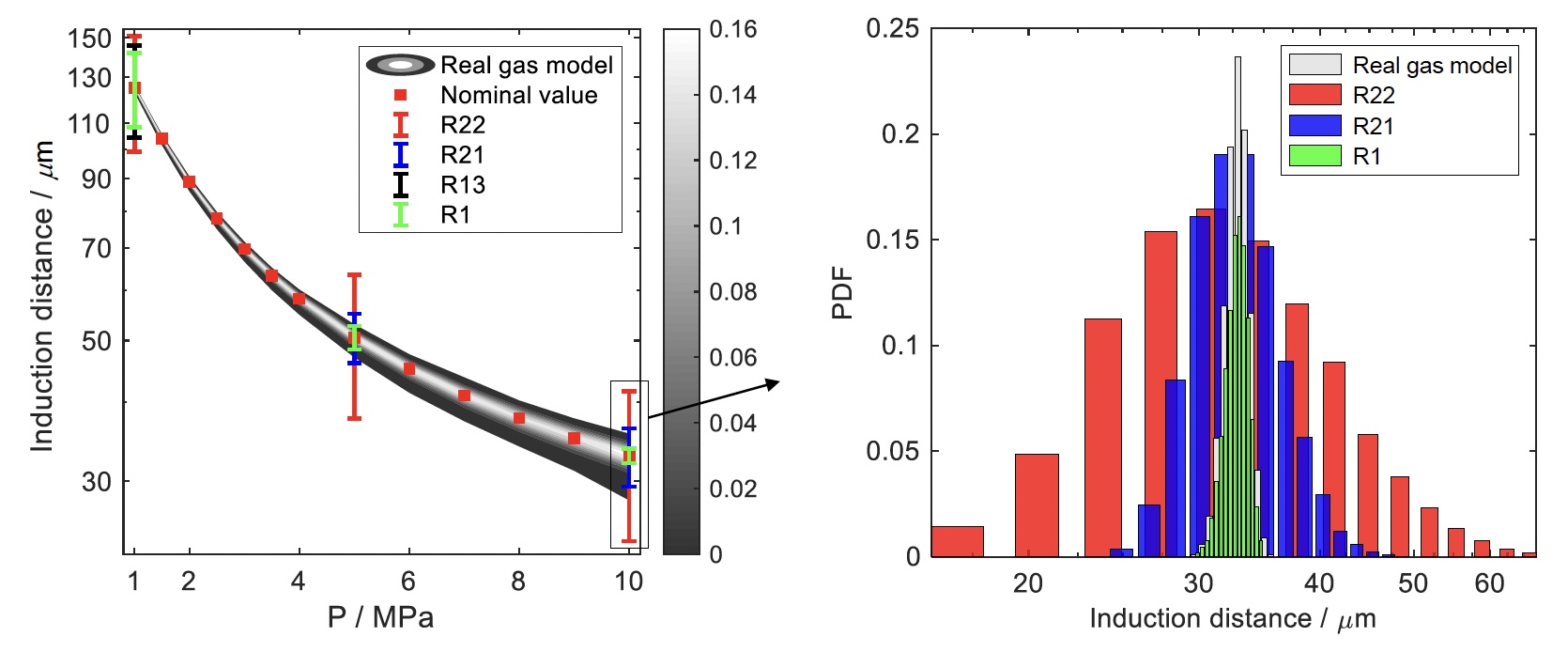
3. Detonation stability
Linear and non-linear stability analysis was performed for 1D detonation for Noble-Abel gas. The finite molecular volume effect stabilizes detonation except for newtonian and weak heat release regimes. Linear stability solutions agree well with numerical simulations.
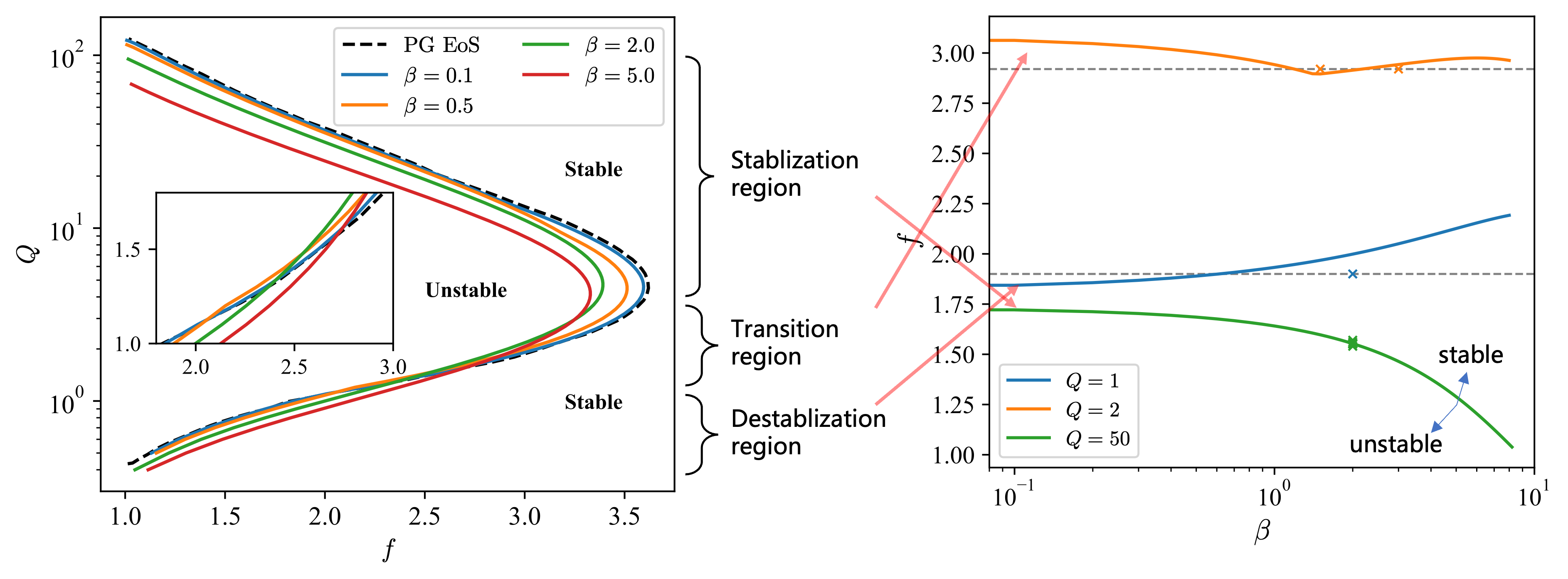
Recently, the study was extended to 2D cellular detonation. More results are coming.
[1] R.G. Schmitt, and P.B. Butler, “Detonation Properties of Gases at Elevated Initial Pressures,” Combustion Science and Technology 106(1–3), 167–191 (1995). [2] S. Taileb, J. Melguizo-Gavilanes, and A. Chinnayya, “Influence of the equation of state on the cellular structure of gaseous detonationsat elevated pressures.pdf,” (2020). [3] L. He and P. Clavin, “On the direct initiation of gaseous detonations by an energy source,” Journal of Fluid Mechanics 277, 227–248 (1994). [4] C.A. Eckett, J.J. Quirk, and J.E. Shepherd, “The role of unsteadiness in direct initiation of gaseous detonations,” Journal of Fluid Mechanics 421, 147–183 (2000).
