Hydrogen Safety | Zifeng Weng

Hydrogen is viewed as a promising energy carrier worldwide in the perspective of the carbon-neutrality goal. The reactive nature of hydrogen involving wide flammability range, low ignition energy and fast flame speed poses the risk of ignition and explosion. The ongoing research aims to secure the safe deployment of hydrogen technologies.

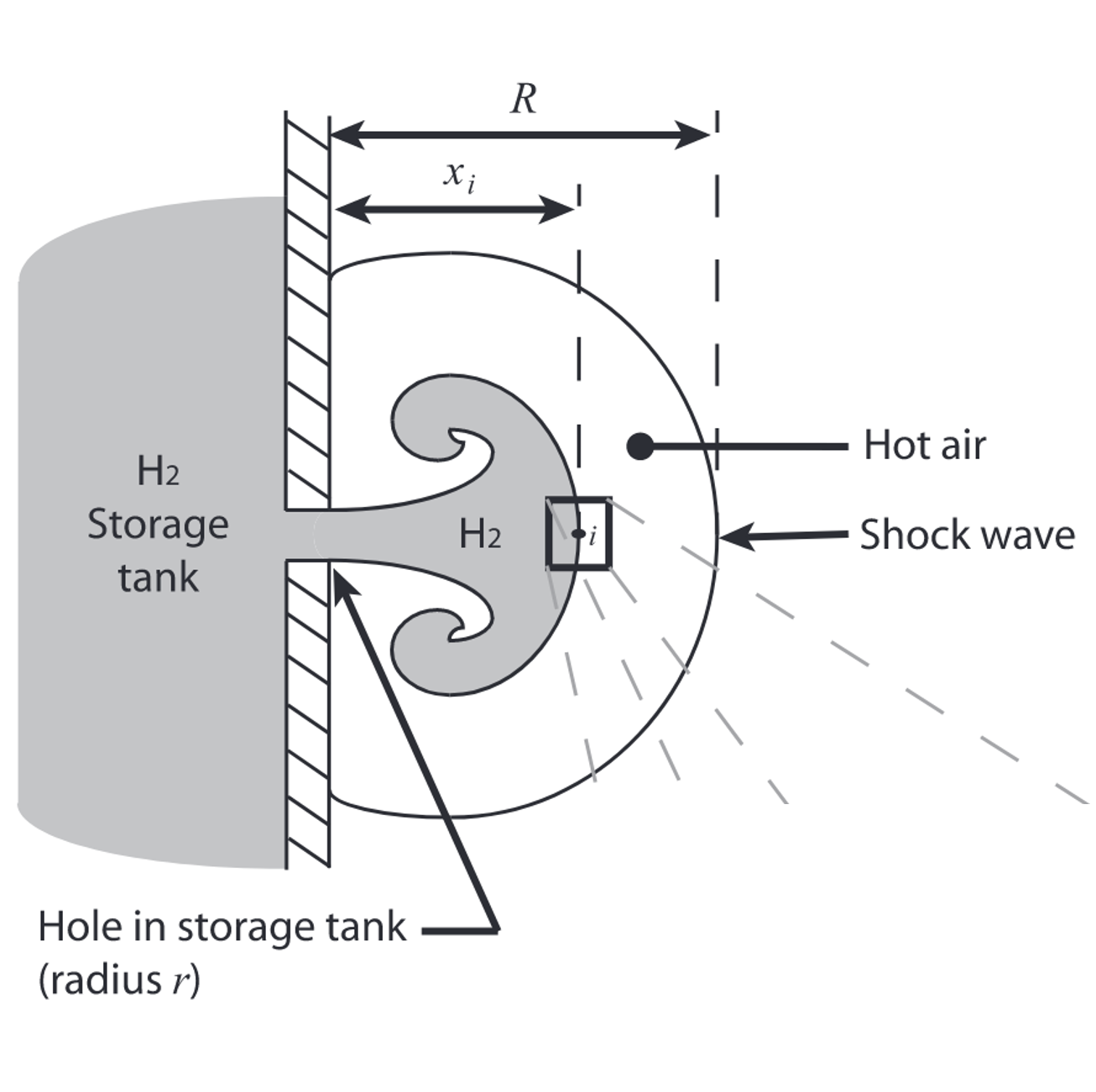
Spontaneous ignition of hydrogen jet

Due to the low volumetric energy density, compressing hydrogen to elevated pressure, i.e., 350 to 700 atm, constitutes a competitive approach for the storage and delivery. However, the spontaneous ignition of hydrogen accidentally released from pressurized equipment poses safety risk to the utilization of hydrogen. A real gas based low-order model is developed by extending Maxwell and Radulescu's work (Combustion and Flame 158, 2011). The problem is simplified as the ignition of a diffusion layer at the jet head.

Accidental release of hydrogen from a high pressure storage tank and the diffusion layer at the jet head (adapted from Maxwell and Radulescu, Combustion and Flame 158, 2011)

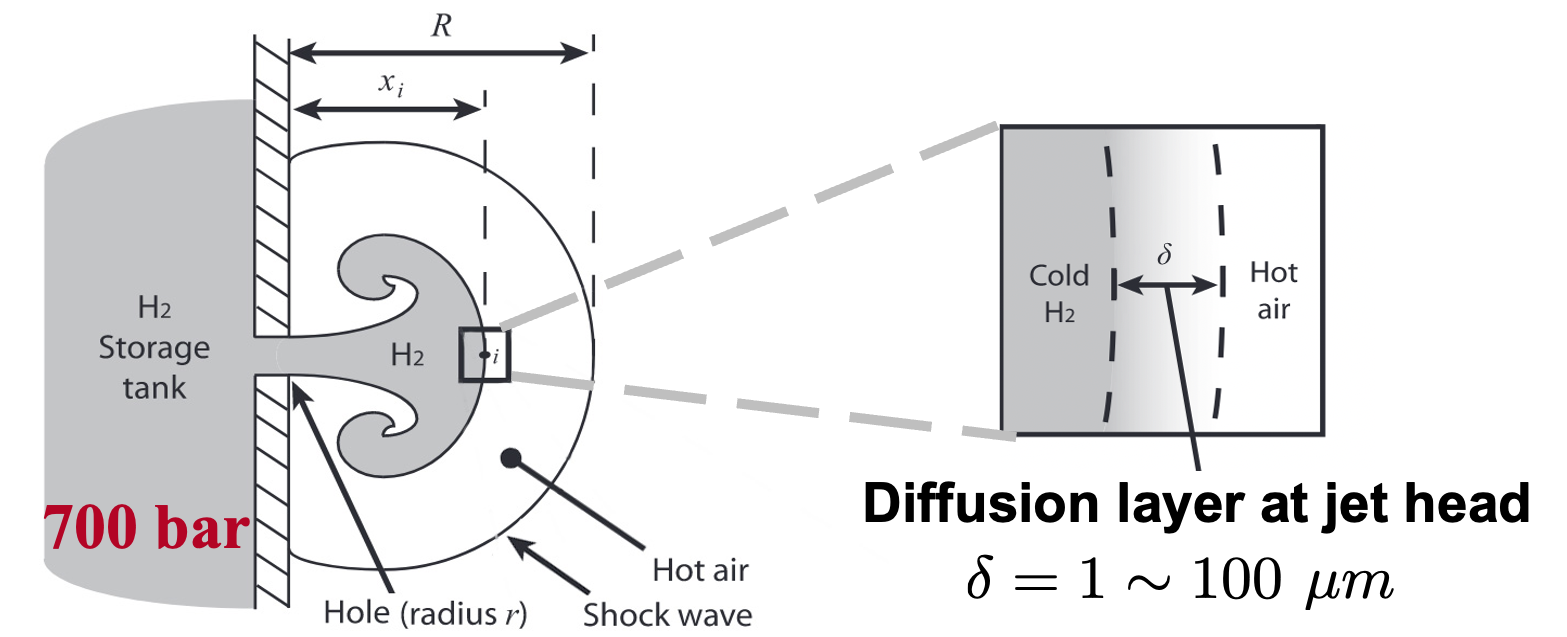
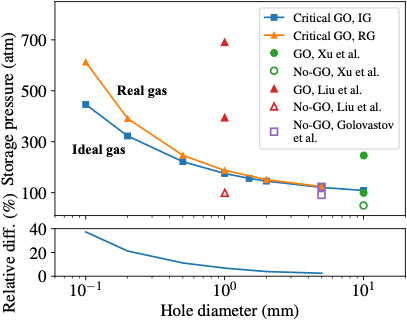
The critical pressure of spontaneous ignition was determined. The results demonstrate satisfactory agreement with experimental data. In unconfined releases, real gas effects lead to higher critical pressures. The relative difference was 10% for a 0.6 mm hole and increased drastically as the hole size was decreased.

Critical storage pressure for successful spontaneous ignition from unconfined release of hydrogen.

Laminar flame speed

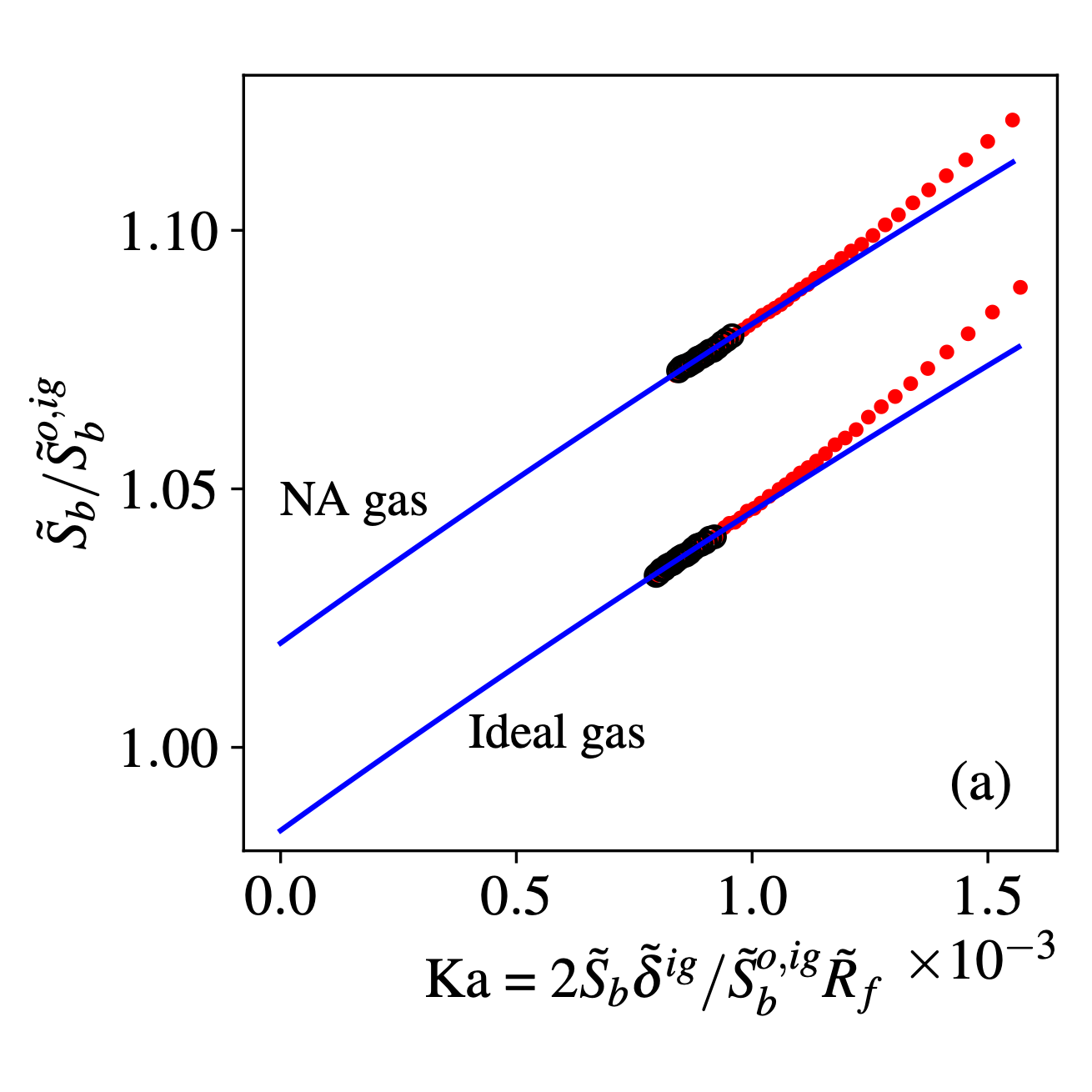
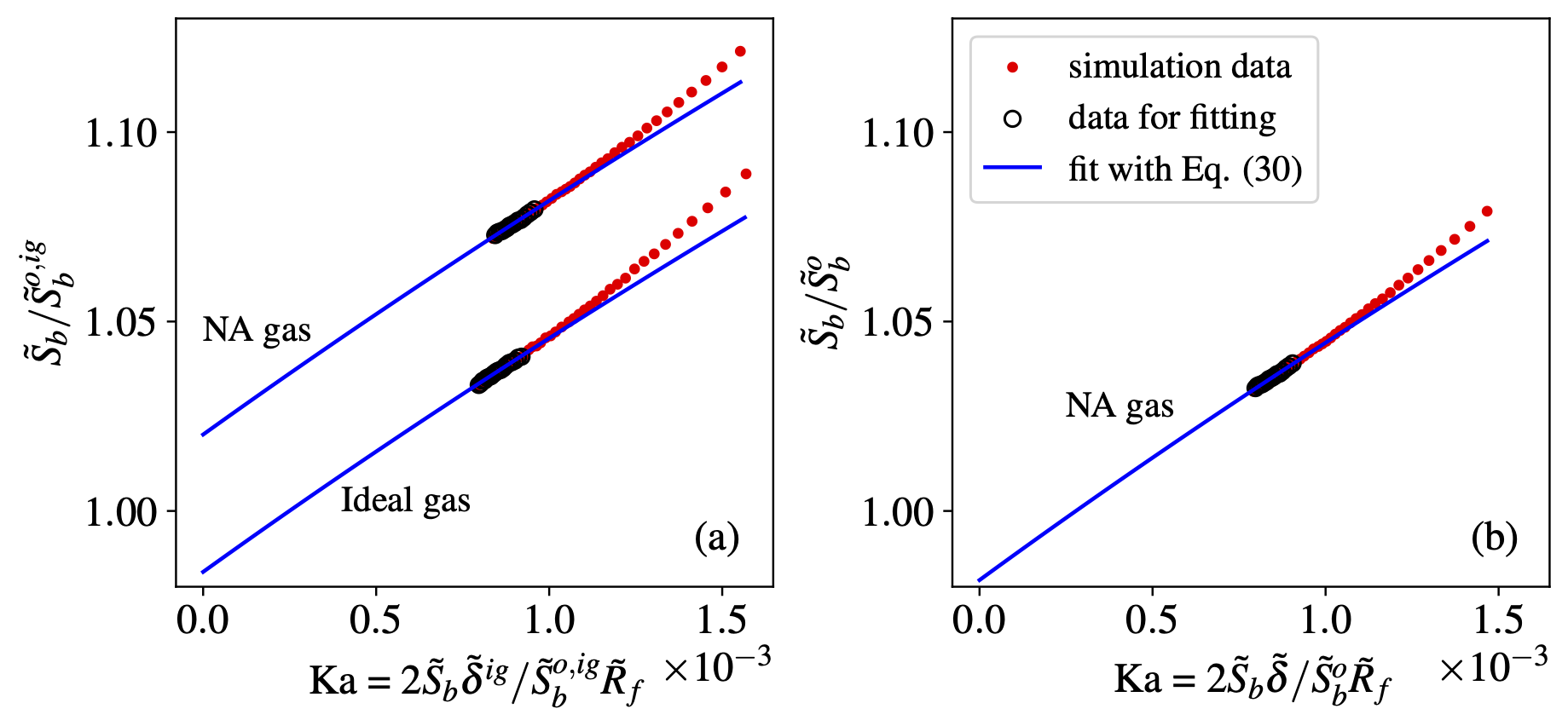
At high pressure, the real gas effects should be considered for the laminar flame speed, a fundamental combustion property for hydrogen flame. Relation between stretch rate and flame speed was derived via asymptotic analysis and Noble-Abel model.

\begin{equation} \label{eq:Evolution_S_R} \left(\frac{S}{1+b}\right)^{2}\ln\left(\frac{S}{1+b}\right)^{2} = -\frac{d}{dR}\left(\frac{S}{1+b}\right) + \frac{2}{R}\left(\frac{S}{1+b}\right) -\frac{d}{dR}\left(\frac{S}{1+b}\right) -l. \end{equation}

The Markstein length (number) was given as

\begin{equation} L_{b} = -\frac{\delta_{ad}I\beta}{2}= -\frac{\delta_{ad}\beta}{2}\int_{\varepsilon}^{1} \frac{1+b}{T^{0}+b}\left[\left(\frac{T^{0}-\varepsilon}{1-\varepsilon}\right)^{\mathrm{Le}-1}-1\right] {\rm d} T^{0}. \end{equation}

The extrapolation relation was validated with spherical flame simulation based on recently developed solver for real gas laminar flame.

The variations of flame speed with the Karlovitz number simulated with IG and NA EoS. The fresh mixture was stoichiometric H2-air.

Related publications

Real gas effects on the dynamics of a reactive diffusion layer: Application to the study of spontaneous ignition limit of pressurized hydrogen jet

Zifeng Weng , Yaqin Tan , Brian Maxwell , and 1 more author

Proceedings of the Combustion Institute, 2024

Bib HTML PDF

@article{jetignition2024,
  title = {Real gas effects on the dynamics of a reactive diffusion layer: Application to the study of spontaneous ignition limit of pressurized hydrogen jet},
  author = {Weng, Zifeng and Tan, Yaqin and Maxwell, Brian and M{\'e}vel*, R{\'e}my},
  year = {2024},
  volume = {40},
  pages = {105370},
  journal = {Proceedings of the Combustion Institute},
}

The effect of finite molecular volume on the propagation of unsteady spherical flame front

Zifeng Weng , Yakun Zhang , Brian M. Maxwell , and 1 more author

Combustion and Flame, 2024

Bib HTML PDF

@article{SphericalFlame2024,
  title = {The effect of finite molecular volume on the propagation of unsteady spherical flame front},
  author = {Weng, Zifeng and Zhang, Yakun and M. Maxwell, Brian and M{\'e}vel*, R{\'e}my},
  year = {2024},
  journal = {Combustion and Flame},
  volume = {263},
  pages = {113404},
}

References

[1] P.D. Ronney, and G.I. Sivashinsky, “A Theoretical Study of Propagation and Extinction of Nonsteady Spherical Flame Fronts,” SIAM J. Appl. Math. 49(4), 1029–1046 (1989).